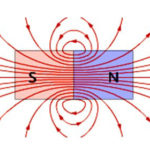
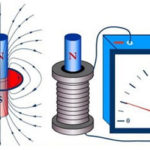
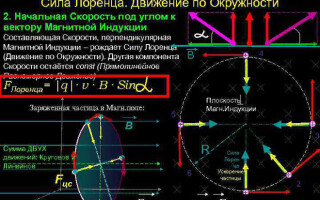
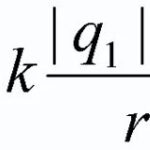Força de Lorentz e a regra da mão esquerda. Movimento de partículas carregadas em um campo magnético

Colocado em um campo magnético condutorpor onde passou eletricidade, é afetado pela força de Ampere $F_A$ , e seu valor pode ser calculado usando a seguinte fórmula:

$F_A=B\cdot I\cdot l\cdot sin\alpha$ (1)

Onde $EU$ e $eu$ - intensidade da corrente e comprimento do condutor, $B$ - indução de campo magnético, $\alfa$ - o ângulo entre as direções da intensidade da corrente e a indução magnética. Por que isso está acontecendo?

Força Lorentz. Movimento de uma partícula carregada em um campo magnético.

Contente

1 Qual é a força de Lorentz - determinando quando ocorre, obtendo a fórmula
2 Determinando a direção da força de Lorentz usando a regra da mão esquerda
3 Movimento de uma partícula carregada em um campo magnético
4 Aplicação da força de Lorentz na engenharia

Qual é a força de Lorentz - determinando quando ocorre, obtendo a fórmula

Sabe-se que a corrente elétrica é um movimento ordenado de partículas carregadas. Também foi estabelecido que durante o movimento em um campo magnético, cada uma dessas partículas é submetida à ação de uma força. Para que uma força ocorra, a partícula deve estar em movimento.

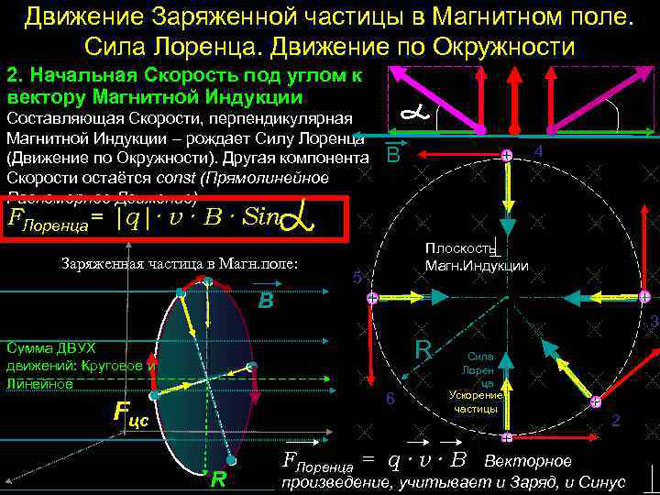
A força de Lorentz é a força que atua sobre uma partícula eletricamente carregada enquanto ela se move em um campo magnético.Sua direção é ortogonal ao plano em que se encontram os vetores da velocidade da partícula e da força do campo magnético. A resultante das forças de Lorentz é a força de Ampère. Sabendo disso, podemos derivar uma fórmula para a força de Lorentz.

O tempo necessário para a partícula passar pelo segmento do condutor, $t = \frac{l}{v}$ , Onde $eu$ - o comprimento do segmento, $v$ é a velocidade da partícula. A carga total transferida durante este tempo através da seção transversal do condutor, $Q = I\cdot t$ . Substituindo aqui o valor do tempo da equação anterior, temos

$Q = \frac {I\cdot l}{v}$ (2)

Ao mesmo tempo $F_A=F_L\cdot N$ , Onde $N$ é o número de partículas no condutor considerado. Em que $N = \frac {Q}{q}$ , Onde $q$ é a carga de uma partícula. Substituindo o valor na fórmula $Q$ de (2), pode-se obter:

$N = \frac {I\cdot l}{v\cdot q}$

Nesse caminho,

$F_A=F_L\cdot \frac {I\cdot l}{v\cdot q}$

Usando (1), a expressão anterior pode ser escrita como

$B\cdot I\cdot l\cdot sin\alpha = F_L\cdot \frac {I\cdot l}{v\cdot q}$

Após as contrações e transferências, aparece uma fórmula para calcular a força de Lorentz

$F_L = q\cdot v\cdot B\cdot sin\alpha$

Dado que a fórmula é escrita para o módulo de força, ela deve ser escrita da seguinte forma:

$F_L = |q|\cdot v\cdot B\cdot sin\alpha$ (3)

Porque o $sin\alpha = sin(180^{\circ} - \alpha)$ , então para calcular o módulo de força de Lorentz, não importa para onde a velocidade é direcionada, - na direção da força da corrente ou contra, - e podemos dizer que $\alfa$ é o ângulo formado pelos vetores velocidade da partícula e indução magnética.

Escrever uma fórmula na forma vetorial ficará assim:

$\vec{F_L} = q\cdot [\vec{v}\times \vec{B}]$

$[\vec{v}\vezes \vec{B}]$ é um produto vetorial, cujo resultado é um vetor com módulo igual a $v\cdot B\cdot sin\alpha$ .

Com base na fórmula (3), podemos concluir que a força de Lorentz é máxima no caso de direções perpendiculares da corrente elétrica e do campo magnético, ou seja, quando $\alfa = 90^{\circ}$ , e desaparecem quando são paralelos ( $\alpha = 0^{\circ}$ ).

Deve-se lembrar que para obter a resposta quantitativa correta - por exemplo, na resolução de problemas - deve-se usar as unidades do sistema SI, em que a indução magnética é medida em teslas (1 T = 1 kg s⁻²·MAS⁻¹), força - em Newtons (1 N = 1 kg m/s²), força atual - em amperes, carga em coulombs (1 C = 1 A s), comprimento - em metros, velocidade - em m / s.

Determinando a direção da força de Lorentz usando a regra da mão esquerda

Como a força de Lorentz se manifesta como a força de Ampère no mundo dos macroobjetos, a regra da mão esquerda pode ser usada para determinar sua direção.

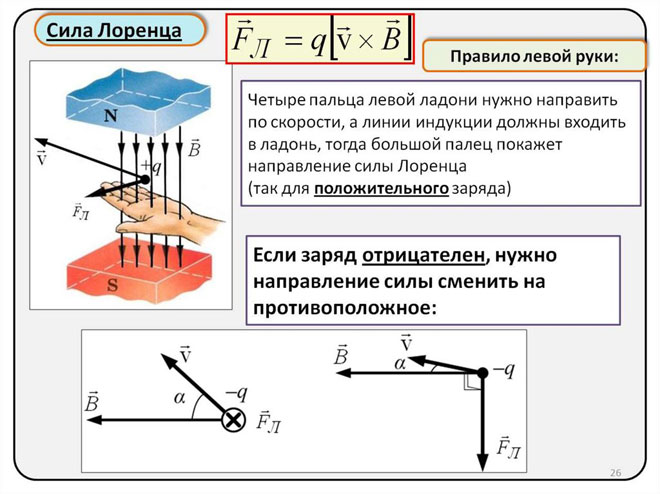
Determinação da direção de ação da força de Lorentz de acordo com a regra da mão esquerda.

Você precisa colocar a mão esquerda para que a palma aberta fique perpendicular e em direção às linhas do campo magnético, quatro dedos devem ser estendidos na direção da força da corrente, então a força de Lorentz será direcionada para onde o polegar aponta, o que deve ser dobrado.

Movimento de uma partícula carregada em um campo magnético

No caso mais simples, ou seja, quando os vetores de indução magnética e velocidade da partícula são ortogonais, a força de Lorentz, sendo perpendicular ao vetor velocidade, só pode mudar sua direção. A magnitude da velocidade, portanto, e a energia permanecerão inalteradas. Isso significa que a força de Lorentz age por analogia com a força centrípeta na mecânica, e a partícula se move em círculo.

De acordo com a lei de Newton II ( $F = m\cdot a$ ) podemos determinar o raio de rotação da partícula:

$N = \frac {m\cdot v}{q\cdot B}$ .

Deve-se notar que com uma mudança na carga específica da partícula ( $\frac {q}{m}$ ) o raio também muda.

Neste caso, o período de rotação T = $\frac {2\cdot \pi\cdot r}{v}$ = $\frac {2\cdot \pi\cdot m}{q\cdot B}$ . Não depende da velocidade, o que significa que a posição mútua das partículas com velocidades diferentes não será alterada.

Movimento de uma partícula carregada em um campo magnético uniforme.

Em um caso mais complicado, quando o ângulo entre a velocidade da partícula e a força do campo magnético é arbitrário, ela se moverá ao longo de uma trajetória helicoidal - translacionalmente devido ao componente de velocidade direcionado paralelamente ao campo e ao longo do círculo sob a influência de seu componente perpendicular.

Aplicação da força de Lorentz na engenharia

Kinescope

O cinescópio, que permaneceu até recentemente, quando foi substituído por uma tela LCD (plana), em todos os aparelhos de TV, não poderia funcionar sem a força de Lorentz. Para formar um raster de televisão na tela a partir de um estreito fluxo de elétrons, são usadas bobinas defletoras, nas quais é criado um campo magnético linearmente variável. As bobinas horizontais movem o feixe de elétrons da esquerda para a direita e o devolvem, as bobinas pessoais são responsáveis pelo movimento vertical, movendo o feixe que corre horizontalmente de cima para baixo. O mesmo princípio é usado em osciloscópios - dispositivos utilizados para estudar a tensão elétrica alternada.

espectrógrafo de massa

Um espectrógrafo de massa é um dispositivo que usa a dependência do raio de rotação de uma partícula carregada em sua carga específica. O princípio de seu funcionamento é o seguinte:

A fonte de partículas carregadas, que ganham velocidade com a ajuda de um campo elétrico criado artificialmente, é colocada em uma câmara de vácuo para excluir a influência das moléculas de ar. Partículas voam para fora da fonte e, tendo passado ao longo do arco de um círculo, atingem a chapa fotográfica, deixando vestígios nela. Dependendo da carga específica, o raio da trajetória muda e, portanto, o ponto de impacto. Esse raio é fácil de medir e, conhecendo-o, você pode calcular a massa da partícula. Com a ajuda de um espectrógrafo de massas, por exemplo, estudou-se a composição do solo lunar.

Ciclotron

A independência do período e, portanto, a frequência de rotação de uma partícula carregada de sua velocidade na presença de um campo magnético, é usada em um dispositivo chamado cíclotron e projetado para acelerar partículas a altas velocidades. Um ciclotron são dois semi-cilindros de metal oco - um dee (em forma, cada um deles se assemelha à letra latina D) colocados com lados retos um para o outro a uma curta distância.

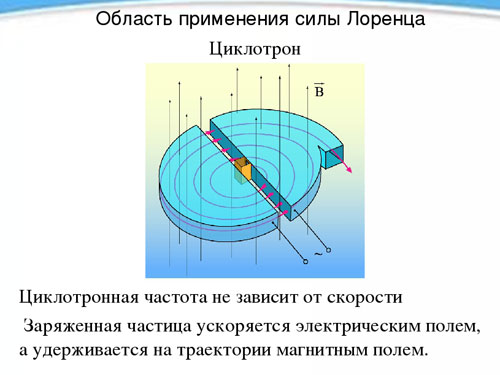
Ciclotron - aplicação da força de Lorentz.

Os dees são colocados em um campo magnético uniforme constante, e um campo elétrico alternado é criado entre eles, cuja frequência é igual à frequência de rotação da partícula, determinada pela força do campo magnético e carga específica. Ficando duas vezes durante o período de rotação (durante a transição de um dee para outro) sob a influência de um campo elétrico, a partícula acelera a cada vez, aumentando o raio da trajetória e, em determinado momento, ganhando a velocidade desejada, voa para fora do dispositivo através do orifício. Desta forma, um próton pode ser acelerado a uma energia de 20 MeV (megaelétron-volt).

Magnetron

Um dispositivo chamado magnetron, que é instalado em cada forno de micro-ondas, é outro representante de dispositivos que usam a força de Lorentz. O magnetron é usado para criar um poderoso campo de micro-ondas, que aquece o volume interno do forno, onde os alimentos são colocados. Os ímãs incluídos em sua composição corrigem a trajetória do movimento dos elétrons dentro do dispositivo.

campo magnético da Terra

E na natureza, a força de Lorentz desempenha um papel extremamente importante para a humanidade. Sua presença permite que o campo magnético da Terra proteja as pessoas da radiação ionizante mortal do espaço. O campo não permite que partículas carregadas bombardeiem a superfície do planeta, forçando-as a mudar de direção.

Artigos semelhantes: